INVESTIGACION DE OPERACIONES II: febrero 2019

Resultado de imagen para DIBUJO ANIMADO HACIENDO TAREAS

PRIMER TALLER

INVESTIGACIÓN OPERACIONES II

PRIMER TALLER

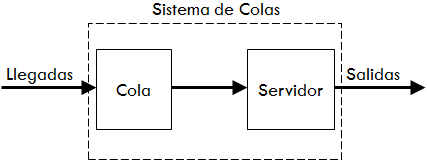
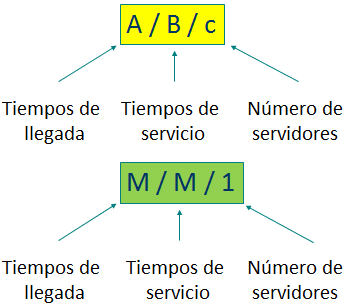
TEMA: LINEAS DE ESPERA Y SISTEMAS DE UN CANAL Y MÚLTIPLES CANALES.

1.1 Doña PEPA, vendedora de comidas, imagina un restaurante de comidas rápidas al cual llegan en promedio 100 clientes por hora. Se tiene capacidad para atender en promedio a 150 clientes por hora. Se sabe que los clientes esperan en promedio 2 minutos en la cola. Calcular:

a) ¿Cuál es la probabilidad que el sistema esté ocioso?

b) ¿Cuál es la probabilidad que un cliente llegue y tenga que esperar, porque el sistema está ocupado?

c) ¿Cuál es el número promedio de clientes en la cola?

d) ¿Cuál es la probabilidad que hayan 10 clientes en la cola?

2.2 En el negocio de don PEPE, un promedio de 10 automóviles por hora llegan a un cajero con un solo servidor que proporciona servicio sin que uno descienda del automóvil. Suponga que el tiempo de servicio promedio por cada cliente es 4 minutos, y que tanto los tiempos entre llegadas y los tiempos de servicios son exponenciales. Conteste las preguntas siguientes: a. ¿Cuál es la probabilidad que el cajero esté ocioso? b. ¿Cuál es el número promedio de automóviles que están en la cola del cajero? (se considera que un automóvil que está siendo atendido no está en la cola esperando) c. ¿Cuál es la cantidad promedio de tiempo que un cliente pasa en el estacionamiento del banco, (incluyendo el tiempo de servicio)? d. ¿Cuántos clientes atenderá en promedio el cajero por hora?

3.3 En la Clínica MARLY, al departamento de emergencia, los pacientes llegan con una distribución de probabilidad Poisson a una media de 3 clientes por hora. El médico que está en dicho departamento los atiende con una frecuencia de servicio exponencial a una tasa media de 4 clientes por hora. ¿Contrataría o no a un segundo médico? Determine:

a. Razón de utilización del sistema (ρ).

b. Probabilidad de que no se encuentren pacientes en el sistema.

c. Probabilidad de que existan 3 pacientes en el sistema ( P3).

d. Tiempo total del cliente en el sistema (Ws).

e. Tiempo total de espera por en la cola (Wq).

f. EI número de pacientes en el sistema en un momento dado (Ls).

g. EI número de pacientes en el sistema esperando por servicio (Lq).

h. Probabilidad de que el cliente se espere más de 1 hora en el sistema [Ws > 1]

4.4 En la ESTACIÓN DE SERVICIO DON JOE, durante un período de 8 horas, llegaron 96 carros a la estación de servicio de Joe. Suponiendo que el tiempo entre llegadas tiene una distribución exponencial, use los datos proporcionados para estimar:

a) El valor de la frecuencia de llegadas.

b) El tiempo medio entre llegadas.

c) La razón media de llegadas

5.5 En el centro de cómputo de la Universidad ECCI, una computadora procesa los trabajos que se le asignan sobre la base "primero en llegar primero ser atendido (FIFO=PEPS). Los trabajos llegan con una distribución Poisson con promedio de tiempo entre llegadas de cinco minutos. En el procesamiento de los trabajos consiste en que ningún trabajo pase más de seis minutos promedio en el sistema. ¿Qué tan rápido debe de trabajar el procesador para cumplir con este objetivo?

6.6 En el negocio llamado LA BOMBA ATÓMICA, actualmente una gasolinera tiene 2 bombas y está considerando agregar una tercera. Los vehículos llegan al sistema con un promedio de 1 cada 10 minutos, cada vehículo requiere de un promedio de 5 minutos para ser atendido. Supóngase que los vehículos llegan de acuerdo con una distribución Poisson y que el tiempo necesario para prestar el servicio se distribuye en forma exponencial.

a) Determine la razón de utilización del sistema. ( ρ )

b) ¿Cuál sería el efecto sobre la línea de espera si se agrega una tercera bomba?

7.7 En el taller LOS TRES CHIFLADOS, tres mecánicos atienden un pequeño taller de reparación de motores. A principios de marzo de cada año, las personas traen sus cañas de timón y podadoras de césped para servicio y reparación. El taller está dispuesto a aceptar todas las cañas de timón y podadoras que traigan los clientes. Sin embargo, cuando los clientes nuevos ven el piso del taller tapizado de trabajos en espera, se van a otra parte para un servicio más rápido. El piso del taller puede alojar un máximo de 15 podadoras o cañas de timón, excluyendo las que están en reparación. Los clientes llegan al taller cada 10 minutos en promedio, y a cada mecánico le lleva un promedio de 30 minutos completar cada trabajo. Tanto los tiempos entre llegadas como los de servicio son exponenciales. Determine lo siguiente:

a) El promedio de mecánicos ociosos.

b) La probabilidad de que al menos un mecánico esté ocioso.

c) El promedio de cañas de timón o podadoras en espera de servicio

8.8 En la Frontera de VENEZUELA, le plantean a usted la siguiente situación: Considere una oficina venezolana de inmigración y suponiendo que un modelo de línea de espera básico es una aproximación razonable de la operación, y si la una agente estuviese ocupada todo el tiempo procesaría 120 ingresos durante su turno de 8 horas. Además a su oficina llega un promedio de un ingreso cada 6 minutos, encuentre:

a) El número esperado en el sistema

b) El número esperado en la fila

c) El tiempo previsto de línea de espera

d) El tiempo previsto de espera

e) La probabilidad de que el sistema este vacío

9.9 En una ciudad de México, todos los dueños de automóvil acuden a la gasolinera cuando sus tanques están a la mitad. En el momento actual llega un promedio de 7.5 clientes por hora a una gasolinera que tiene una sola bomba. Se requiere un promedio de 4 minutos para servir a un automóvil. Suponga que los tiempos entre llegadas y los tiempos de servicios son exponenciales.

a) Calcule Ls y Ws para los tiempos actuales.

b) Suponga que hay un déficit de gasolina y que hay compras de pánico. Para modelar este fenómeno, suponga que todos los dueños de automóviles compran ahora gasolina cuando sus tanques tienen ¾ de combustible. Como cada dueño pone ahora menos gasolina en el tanque cada vez que acude a la gasolinera, supongamos que el tiempo de servicio promedio se reduce a 3 minutos y un tercio, y λ=2(7.5)= 15 automóviles por hora.

Qué tanto afectan a L y W las compras de pánico?